AXEC: New Foundations of Economics: Putting the Quantity Theory of inflation to rest

March 13, 2021

Putting the Quantity Theory of inflation to rest

Comment on Blair Fix on ‘Energizing exchange: Learning from econophysics’ mistakes’

Macroeconomics is provably false since Keynes.#1 The correct macrofoundations are given with this set of axioms: (A0) The objectively given and most elementary configuration of the economy consists of the household and the business sector which in turn consists initially of one giant fully integrated firm. (A1) Yw=WL wage income Yw is equal to wage rate W times working hours. L, (A2) O=RL output O is equal to productivity R times working hours L, (A3) E_c=PX consumption expenditure Ec is equal to price P times quantity bought/sold X.

Under the conditions of market-clearing X=O and budget-balancing E_c=Y_w in each period the price as dependent variable is given by P=W/R, i.e. the market-clearing price is equal to unit wage costs. This is the most elementary form of the macroeconomic Law of Supply and Demand. For the graphical representation see Wikimedia AXEC31a

The macroeconomic price is determined by the wage rate W, which takes the role of the nominal numéraire, and the productivity R. The quantity of money is NOT among the price determinants.

Monetary profit for the economy as a whole is defined as Q_m≡E_c−Y_w and monetary saving as S_m≡Y_w−E_c. It always holds that the sectoral balances add up to zero, i.e. Q_m+S_m=0. In other words, the business sector’s deficit=loss equals the household sector’s surplus=saving and vice versa, the business sector’s surplus=profit equals the household sector’s deficit=dissaving. This is the most elementary form of the macroeconomic Profit Law. Under the condition of budget-balancing E_c=Y_w, monetary profit is zero.

What is needed next is two things (i) a Central Bank which creates money on its balance sheet in the form of deposits, and (ii), a legal system that declares the Central Bank’s deposits as legal tender. These conditions define a fiat money system without commercial banks as intermediaries.

Deposit money is needed by the business sector to pay the workers who receive the wage income Y_w per period. The need is only temporary because the business sector gets the money back if the workers fully spend their income, i.e. if E_c=Y_w.

Overdrafts are needed by the household sector for consumption expenditures if the households want to spend before they get their wage income. This time sequence is no problem for the Central Bank because the temporary overdrafts vanish with wage payments.

For the case of a balanced budget C=Y_w, the idealized transaction sequence of deposits/overdrafts of the household sector at the Central Bank over the course of one period is shown on Wikimedia AXEC98

The household sector’s deposits/overdrafts are zero at the beginning and end of the period. The business sector’s transaction pattern is the exact mirror image. Money, that is, deposits at the Central Bank, is continually created and destroyed during the period under consideration. There is NO such thing as a fixed quantity of money. The central bank plays an accommodative role and simply supports the autonomous market transactions between the household and the business sector.

From this follows the average stock of transaction money as M=κY_w, with κ determined by the transaction pattern. In other words, the average stock of money M is determined by the autonomous transactions of the household and business sector and created out of nothing by the Central Bank. The economy never runs out of money.

The transaction equation reads M=κY_w=κE_c=κPRL in the case of budget balancing and market clearing, and this yields the commonplace correlation between the average stock of money M and price P for a given employment level L and productivity R, except for the fact that M is the dependent variable. If P doubles, M doubles, and P doubles if W doubles with the real variables L and R fixed.

Inflation ensues under the conditions of market clearing and budget-balancing if the wage rate rises faster than the productivity and deflation ensue in the opposite case. Under the condition of L and R constant, one always gets the commonplace correlation between the average stock of money M and price P with the causality running from P to M.

For the general case, the elementary macroeconomic price formula states P=ρ_EW/R with ρ_E≡E_c/Y_w. ρ_E>1 represents deficit-spending and this implies that a period deficit produces a one-off price hike. So, if ρ_E=1 in the initial period and ρ_E=2 in the next period then the price doubles.

The transaction equation reads for the general case M=κ sup {Y_w, E_c} or M=κ sup {1, ρ_E}Yw and this means that if E_c is greater than Y_w then E_c determines the quantity of transaction money. So, if E_c doubles, i.e. ρ_E=2, then M doubles. In this case, the old Quantity Theory correlation between P and M reappears.

However, this does NOT lead to inflation as a process over multiple periods. If ρ_E=2 again in the next period, then the price P remains at the elevated level but does not rise further. So, the continuous deficit spending of the household sector does NOT cause inflation. (Only successive increases of the expenditure ratio ρ_Elead to successive price hikes.)

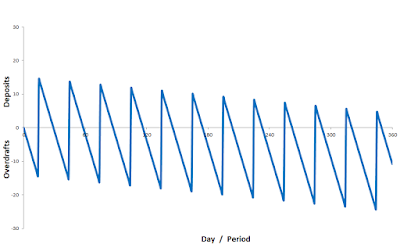
However, the average stock of transaction money increases continuously.#2 The transaction pattern in the case of continuous dissaving is shown on Wikimedia AXEC99

As a mirror image, the deposits of the business sector at the Central Bank increase continuously because the profit of the business sector is equal to the dissaving/deficit-spending of the household sector. So, the average quantity of money in the system increases continuously but the price remains stable at the elevated level for a given ρ_E. There is NO proportionality between M and P and this means that the commonplace Quantity Theory is refuted.

Egmont Kakarot-Handtke

#1 Macroeconomics without Keynes

#2 Money and time

Additional link: Michael D. Bordo and Mickey D. Levy, Do Enlarged Fiscal Deficits Cause inflation: The Historical Record

Knowledge only — no opinion

Science does not explain everything, but non-science explains nothing.

Neither orthodox nor heterodox economics satisfies the scientific criteria of material and formal consistency.

Economists cannot explain how the economy works. The Profit Theory is false since Adam Smith. There is much opinion and little knowledge.

Opinion is the realm of political economics, knowledge is the realm of theoretical economics.

Political economics is scientifically worthless.

Theoretical economics is built upon clearly stated premises, i.e., upon a set of axioms.

Orthodoxy got the axiomatic foundations wrong and Heterodoxy has none at all.

Economics is a failed science. Economists are incompetent scientists.

Profit

Neither Classicals, nor Walrasians, nor Marshallians, nor Marxians, nor Keynesians, nor Institutionialists, nor Monetary Economists, nor MMTers, nor Austrians, nor Sraffaians, nor Evolutionists, nor Game theorists, nor EconoPhysicists, nor RBCers, nor New Keynesians, nor New Classicals ever came to grips with profit. Hence, they all fail to capture the essence of the market economy.

Because of this, economists have nothing to offer in the way of a scientifically founded economic policy guidance.

The hybrid science

As a first approximation, one can agree on the general characteristic that the economy is a complex system.

However, with the term system one usually associates a structure with components that are non-human. In order to stress the obvious fact that humans are an essential component of the economic system the market economy should be characterized more precisely as a complex hybrid human/system entity.

The scientific method is straightforwardly applicable to the sys-component but not to the hum-component. While it is clear that the economy always has to be treated as an indivisible whole, for good methodological reasons the analysis has to start with the objective system-component.

In gestalt-psychological terms the economic system is the foreground, individual behavior the background. Common sense wrongly insists that the hum-component must always be in the foreground. This fallacy compares to geo-centrism. The economic system has its own logic which is different from the behavioral logic of humans. The systemic logic is what Adam Smith called the Invisible Hand.

There are systemic laws but no behavioral laws. Systemic laws have the same methodological status as physical laws.

Neither Orthodoxy nor Heterodoxy can tell what the systemic laws of the actual monetary economy are.

Whether the outcome of the human/system-interaction is good or bad is a politcal question that lies outside of theoretical economics. Theoretical economics explains how the actual economy works - no less, no more.

Narrative vs.Theory

Psychological, sociological or behavioral assumptionism cannot yield anything other than a gossip model of the world. Second-guessing the agents is not economic analysis.

Science deals exclusively with propositions that can in principle be decided by objective means. The rest is opinion, faith, phantasy, motive speculation, allegation, hallucination, myth, paranoia, ink-blot association, psychology, philosophy, in one word: storytelling.

Storytelling is the original mode of communication in the social realm — except science.

Political economics is storytelling and, by default, the natural habitat of confused confusers. Walrasianism, Keynesianism, Marxianism, Austrianism are social narratives and not scientifically valid representations of reality.

"The truth is, most persons, not excepting professional economists, are satisfied with very hazy notions." (Fisher)

In marked contrast, theoretical economics lives up to the standards of material and formal consistency. A scientific theory is the best mental representation of reality that is humanly possible.

Theory starts with a set of objective and consistent axioms.

Paradigm Shift

"The problem is not just to say that something might be wrong, but to replace it by something — and that is not so easy." (Feynman)

"As will become evident, there is more agreement on the defects of orthodox theory than there is on what theory is to replace it: but all agreed that the point of the criticism is to clear the ground for construction." (Nell)

"The moral of the story is simply this: it takes a new theory, and not just the destructive exposure of assumptions or the collection of new facts, to beat an old theory." (Blaug)

"Is it not a fact, which stares at us from the histories of all sciences, that it is much more difficult for the human mind to forge the most elementary conceptual schemes than it is to elaborate the most complicated superstructure when those elements are well in hand?" (Schumpeter)

"The task of producing knowledge against the grain requires imagination." (Mirowski)

"A new idea is extremely difficult to think of. It takes a fantastic imagination." (Feynman)

"The scientific imagination dreams of explanations and laws." (Peirce)

"It is brilliance of imagination which makes the glory of science." (Evans)

"... we know little more now about ‘how the economy works,’ ... than we knew in 1790, after Adam Smith completed the last revision of The Wealth of Nations." (Clower)

Selftest and to watch for

You apply one of these items

• supply-demand-equilibrium,

• general equilibrium,

• marginal utility,

• well-behaved production functions,

• total income = value of output,

• total income = wages + profits,

• I=S,

• wage rate down - employment up,

• behavioral axioms?

Then you are out of science because of unnoticed material or formal inconsistency.

Every economist who uses the concept of equilibrium is scientifically incompetent because she/he failed to notice that equilibrium is an economic nonentity.

Practically this means: as soon as the word equilibrium appears in an economic text it can be thrown into the waste basket. The same holds for all other nonentities.

The vast majority of economists deals mainly with nonentities. This is why Walrasianism, Keynesianism, Marxianism, Austrianism is scientifically worthless.

Since Adam Smith, economic policy guidance has no sound scientific foundations.

To be replaced (1)

The core premises of Orthodoxy are uncertain and false and this fully explains the failure of the research program.

“As with any Lakatosian research program, the neo-Walrasian program is characterized by its hard core, heuristics, and protective belts. Without asserting that the following characterization is definitive, I have argued that the program is organized around the following propositions: HC1 economic agents have preferences over outcomes; HC2 agents individually optimize subject to constraints; HC3 agent choice is manifest in interrelated markets; HC4 agents have full relevant knowledge; HC5 observable outcomes are coordinated, and must be discussed with reference to equilibrium states.” (Weintraub)

The inescapable Paradigm Shift consists of the move from this obsolete hard core to the superior set of structural axioms.

To be replaced (2)

The fundamental equations of macroeconomics have been formulated by Keynes in two lines.

"Income = value of output = consumption + investment. Saving = income - consumption. Therefore saving = investment."

This elementary syllogism is demonstrably false. The demonstration consists in the proof that Keynes could not solve the Profit Puzzle. Neither did Post-Neo-New-Keynesians.

In the most general terms, the economics Paradigm Shift consists in switching from the behavior-centric bottom-up approach to the structure-centric top-down approach. This is comparable to the Copernican turn from geo-centrism to helio-centrism.

Consensus

Economics is a science without scientists. Because they are ignorant of the elementary difference between profit and income, the present generation of economists has not made and cannot make a significant contribution to the discussion about how the actual economy works.

Every orthodox or heterodox economist can convince himself/herself that their profit theory is defective.

Every non-economist can — by applying elementary logic — convince himself that conventional profit theories are false. See 'How the intelligent non-economist can refute every economist hands down'.

Because the profit theory is false the whole of conventional economic theory has to be rejected.

"What is now taught as standard economic theory will eventually disappear, no trace of it will remain in the universities or boardrooms because it simply doesn’t work: were it engineering, the bridge would collapse." (McCauley)

No scientist will ever accept Walrasianism, Keynesianism, Marxianism, or Austrianism. These approaches are logically and/or empirically refuted. This is the actual methodological state-of-art. Walrasians, Keynesians, Marxians, or Austrians are still at the proto-scientific stage. These approaches cannot be improved, only abandoned.

Economists are a public nuisance because they have an opinion on everything but knowledge of nothing.

About me

“Bottom line is that your profit law is just a definition you made up nobody else agrees with, nobody. You are all alone with your precious tautology.” Barkley Rosser

“In any event, your entire theory is based on you doing macro accounting in wacky fashion that nobody agrees with.” Brian Romanchuk

"Your stuff is at least original: it's quite cool after a couple of decades at this to see a fresh Economics. But real promises are not advanced: they were around for millennia until the Greeks obscured them with Metaphysics." Chris Cook

"No mate, they're you-blockers. You have all the personality traits of a crank, and the rest of them have tired of you. You could be 100% right, and you'd still die as your only follower." Steve Keen

"What you are doing fills is all with joy, your constructive critique is most welcome!"

Achim Truger,

German Council of Economic Experts,

in a failed attempt to be ironic

"200+ years of thought and yet you are the only one who gets it—or even understands your argument. Thank god we have you, pseudonymous Twitter user. Otherwise no one would know."

William Luther

Assistant Professor of Economics

in a failed attempt to be funny

"Egmonts profit law is the perfect equation that demonstrates this in action. Put the equation into a spreadsheet and then add government spending and watch how it flows into profits. Enter in some debt (-Sm) and watch too how that flows into profits. It can't go anywhere else."

Dean

About the rest of economics

Walrasianism, Keynesianism, Marxianism, Austrianism, MMT, Pluralism are mutually contradictory, axiomatically false, materially/ formally inconsistent. Economics is a failed science.

“There are three classes of people: those who see. Those who see when they are shown. Those who do not see.” Leonardo da Vinci

In economics, the overwhelming majority belongs to Class III. This explains why economics is after 200+ years still at the proto-scientific level.

The obvious task for every economist is to advance from cargo cult science and political agenda-pushing to science. This is absolutely beyond the means of Class III people.

For 200+ years now, economists are not scientists but agenda pushers, useful idiots, clowns in the political Circus Maximus.

Nopopop

This blog does not add to any popular/un- popular opinion.

This blog does not hand out advice about how to avoid taxes, to get rich on the stock market, to be successful in business, to increase the wealth of nations, to run an economy, to maximize welfare, to prevent national/global bankruptcy, to improve the institutional setup of society, to get out of national/global depression, nor about how to save humankind or any subgroup thereof.

This blog is about the true theory of the actual monetary economy.

"In order to tell the politicians and practitioners something about causes and best means, the economist needs the true theory or else he has not much more to offer than educated common sense or his personal opinion." (Stigum)

Focus

Science is of primary interest and importance. Scientists are of secondary interest.

With regard to science, most people lose focus easily because of a natural preference for anecdotes and gossip over facts or subjectivity over objectivity.

Hence, Schumpeter once considered it necessary to remind his habitually disoriented fellow economists: “Remember: occasionally, it may be an interesting question to ask why a man says what he says; but whatever the answer, it does not tell us anything about whether what he says is true or false.”

Science is about true/false and nothing else.

Disclaimer

Missing Blog-Reference links: AXEC does not guarantee that their comments can at any time be recovered from where they have been posted intitially because the availability depends on the publication policy of the blog owner which is implicitly accepted on entering a debate. See also: 'Economists: Incompetent? Stupid? Corrupt?'

Texts: Parts of arbitrary length of any of the author's texts is and will be used again by the author in papers, books, websites, blogs, and other media without explicit reference. The right to make corrections or minor textual improvements on reutilization is reserved. Therefore, it is always a good idea to double-check for the latest version.

Caution: Do not expect a corroboration of your political view. Neither a refutation. Political economics has been scientifically worthless since Adam Smith. Politics has to be separated from economics because it is categorically different from science. The best science can do and has always done is to prove beyond reasonable doubt that you have been objectively wrong or ignorant until now. Science goes beyond the naive common sense of today and becomes the sophisticated common sense of tomorrow.

See also Terms of Use and Legal at www.AXEC.org

Outlook

To recall, while political economics is storytelling, theoretical economics adheres to scientific standards.

The first task of theoretical economics is to get the axiomatic foundations right. This is what J. S. Mill called the opus magnum. Neither Orthodoxy nor Heterodoxy came up with a reasonable solution to this day. This explains the secular stagnation of economics.

There is no serious alternative to structural axiomatic economics. This is not a matter of opinion but of proof. The sole criteria are material and formal consistency.

All of economics has to be reconstructed from the ground up.

Major economic policy implication

The price mechanism does not work as standard economics hypothesizes. The axiom-based Employment Law states that overall employment increases if the average wage rate increases relative to average price and productivity. This gives one the lever to improve the employment situation all over the world and to fend off deflation without rising debt and without artificial capacity growth. To increase the average price relative to the average wage rate and productivity increases unemployment.

Right policy depends on true theory.

“In order to tell the politicians and practitioners something about causes and best means, the economist needs the true theory or else he has not much more to offer than educated common sense or his personal opinion.” (Stigum)

Lacking the true theory, economists promote for more than 200 years opinion instead of knowledge.